彩票星空娱乐网站

解决方案

用Wolfram语言构建三维勾股树

我国古代把直角三角形称为勾股形，直角边中较小者为勾，另一长直角边为股，斜边为弦，所以把这个定理称为勾股定理。在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，因而西方人都习惯地称这个定理为毕达哥拉斯定理。

勾股树，又称为毕达哥拉斯树。它是由古希腊数学家毕达哥拉斯根据勾股定理画出的一个可以无限重复的图形，因为重复多次以后的形状像一棵树，因此得名。这种图形也被称为分形图。

勾股定理：在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。

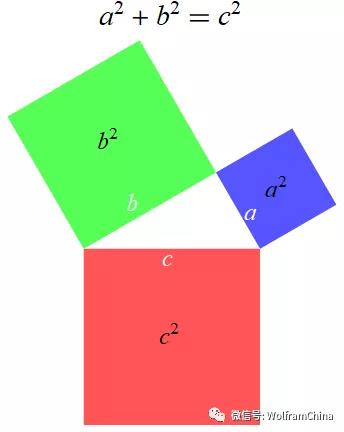
以上图为基础，让两个较小的正方形按勾股定理继续“生长”，又能画出新一的勾股图，如此一直画下去，最终得到一棵完全由勾股定理图组成的树状图形，因此称之为勾股树。

上图展示的是一棵勾股树的前几次生长过程，迭代20次之后的图形如下图所示：

通过改变勾股图中直角三角形的两个锐角的大小，可以构造出不同形状的勾股树。

在Mathematica软件里构造勾股树很简单，方法也有多种，下面就是一种实现，通过平移旋转缩放然后重复迭代。

Clear["`*"];

next[{a_,b_,c_,d_},t_:Pi/6]:=

{

{a,b,c,d}//TranslationTransform[c-b]//RotationTransform[t-Pi/2,c]//ScalingTransform[{1,1}Sin[t],c],

{a,b,c,d}//TranslationTransform[c-b]//RotationTransform[t,d]//ScalingTransform[{1,1}Cos[t],d]

};

pts=NestList[Join@@next/@#&,N@{{{0,0},{1,0},{1,1},{0,1}}},5];

Graphics[Polygon/@pts]

那么有没有三维的勾股树呢，一个自然的想法是把正方形都换成正方体，开始尝试在二维的基础上用RegionProduct函数拓展一个维度，后来发现直接对原始的正方体进行变换也不麻烦嘛，和二维的情况差不多。

Clear["`*"];

next[{a1_,b1_,c1_,d1_,a2_,b2_,c2_,d2_},t_:Pi/6]:=

{

{a1,b1,c1,d1,a2,b2,c2,d2}//TranslationTransform[a2-a1]//RotationTransform[t,{0,-1,0},(a2+d2)/2]//ScalingTransform[{1,1,1}Cos[t],(a2+d2)/2],

{a1,b1,c1,d1,a2,b2,c2,d2}//TranslationTransform[a2-a1]//RotationTransform[Pi/2-t,{0,1,0},(b2+c2)/2]//ScalingTransform[{1,1,1}Sin[t],(b2+c2)/2]

};

n = 15;

pts=NestList[Join@@next/@#&,N@{{{0,0,0},{1,0,0},{1,1,0},{0,1,0},{0,0,1},{1,0,1},{1,1,1},{0,1,1}}},n];

Graphics3D[Hexahedron/@pts]

上面的代码速度有些慢，迭代15次生成数据点耗时大约60s（CPU i7-9750H），我们使用Wolfram语言中的Compile和Listable属性进行加速：

Clear["`*"];

next=

{a1,b1,c1,d1,a2,b2,c2,d2}/.v_:>(

{

v//TranslationTransform[a2-a1]//RotationTransform[-t,{0,1,0},(a2+d2)/2]//ScalingTransform[{1,1,1}Cos[t],(a2+d2)/2],

v//TranslationTransform[a2-a1]//RotationTransform[Pi/2-t,{0,1,0},(b2+c2)/2]//ScalingTransform[{1,1,1}Sin[t],(b2+c2)/2]

}/.

Thread[v->Table[Indexed[A,{x,y}],{x,8},{y,3}]]/.

expr_:>Compile[{{A,_Real,2},{t,_Real}},

expr,RuntimeAttributes->{Listable}

]

);

n=15;

pts=Join@@MapIndexed[Flatten[#,#2[[1]]-1]&,NestList[next[#,Pi/4.]&,N@{{{0,0,0},{1,0,0},{1,1,0},{0,1,0},{0,0,1},{1,0,1},{1,1,1},{0,1,1}}},n]];//AbsoluteTiming

Graphics3D[{EdgeForm[],Hexahedron@pts},ImageSize->Full]

代码优化之后，迭代15次只需0.03秒，比原来提速2000倍。迭代20次生成数据点也不到一秒，但此时的瓶颈是画图速度了。

随着迭代次数的增加，图形的变化：

如果把初始的正方体改成圆柱，看起来是不是更像树了？

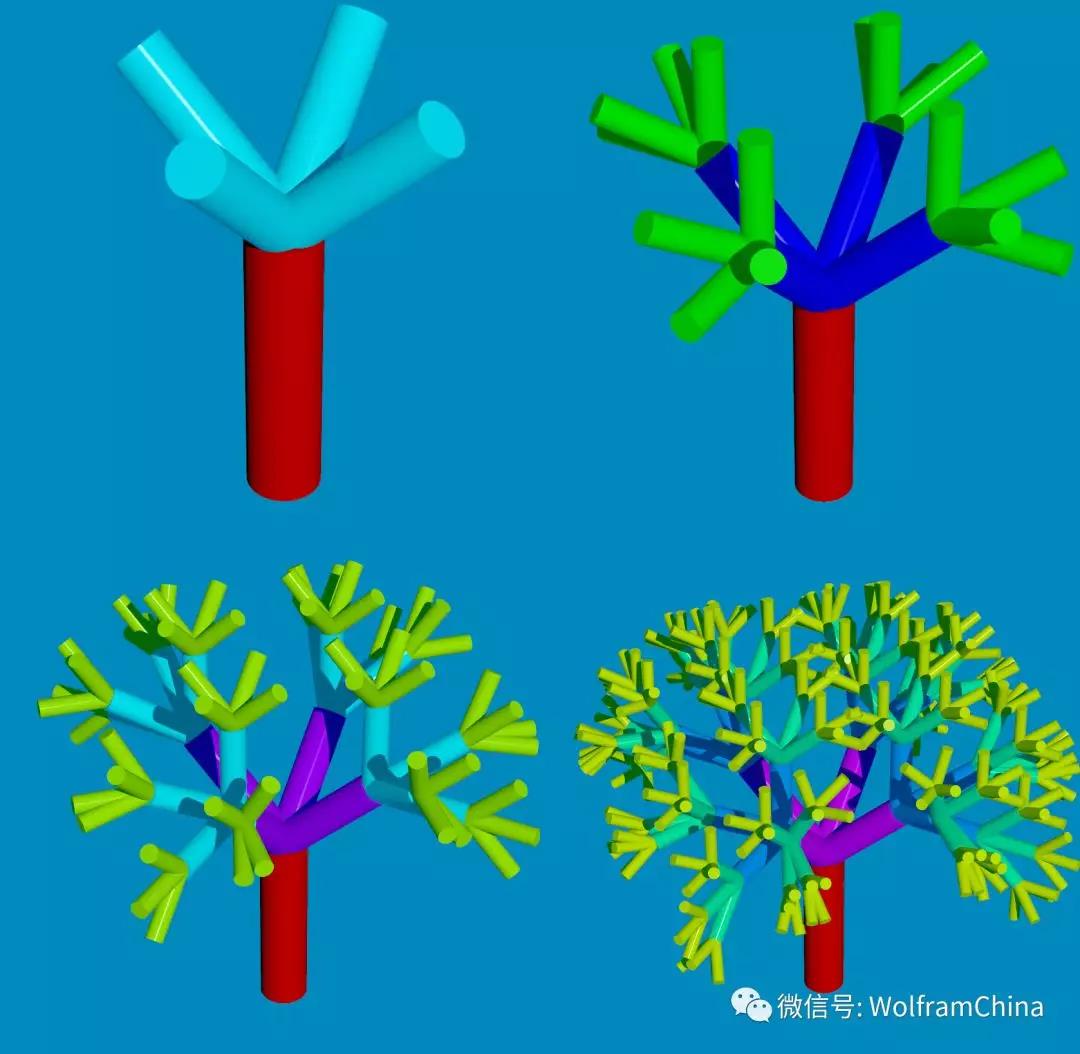
你喜欢哪种配色？

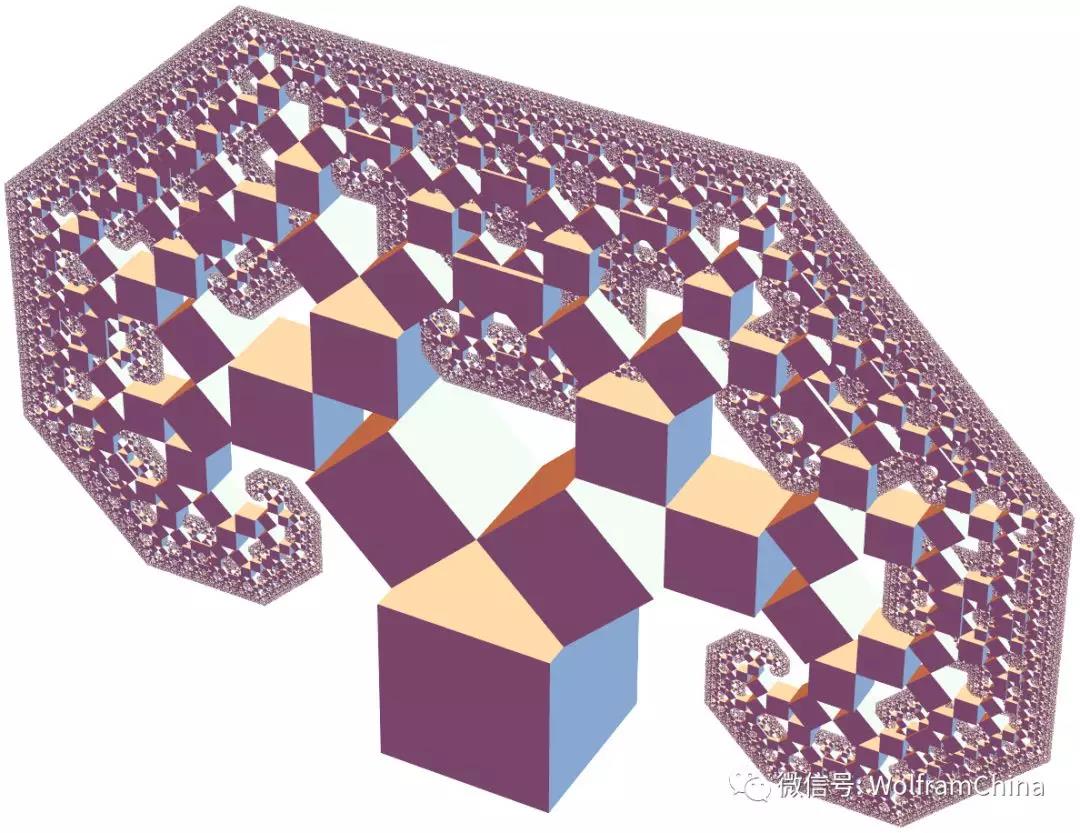
迭代22次的图形：